seamless tileset template II
Author:
Thursday, June 12, 2014 - 09:40
Art Type:
License(s):
Collections:
Favorites:
29
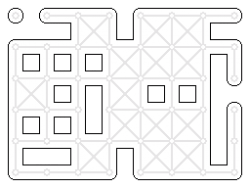
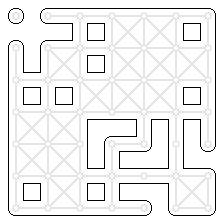
These are variants of http://opengameart.org/content/seamless-tileset-template and http://opengameart.org/content/wang-%E2%80%98blob%E2%80%99-tileset with fewer duplicate tiles. See there for more explanation.
There is a 8x6 variant with only one duplicated tile and a 7x7 variant with two duplicates. As 47 is prime, even fewer duplicates are impractical.
I hereby license the templates and the first preview tileset under CC0.
Copyright/Attribution Notice:
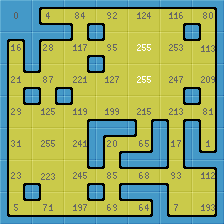
The second and fourth preview are based on CC0 work by http://opengameart.org/users/guy with the following copyright/attribution notice:
Not required, though a link to appropriate cr31 webpage appreciated.
File(s):







Comments
Brilliant. Quite amazing. I’ll use these layouts for future Blob tile layout designs at cr31. Many thanks for your work.
Thanks a lot for the submission!!!
I'm using it in my Mazer project for minimap generation https://www.youtube.com/watch?v=CPxa9If__8s & https://www.youtube.com/watch?v=PsFleC1KBe8
You could make use of the actual example tileset? That's certainly unexpected. So we have another good point for (software) freedom: Allowing good things to happen that oneself does not think of.
I will add an explicit license grant for the tileset in a moment.
Good luck with your project.
Wow... I didn't think anything else was availalbe :D But, yes... I'm using a modified template7x7.png file as an atlas for the minimap tiles :)
P.S. Maybe somebody will get use of the modified tiles? I've also had to make over 200 lines of code to make them work together with the in-game map...
By adding one more tile the 8x6 is fully filled. Inverse of the new tile also may be added instead. (Possibly both may be added to 7x7 version, but it is not straight forward). Nontheless, thanks for great job. Your image inspired me to rethink tiling - but, for now I will use 16 tiles version (scheme attached, no "roads", less data and easier to automate in-game generation/editing).
@ mawigator:
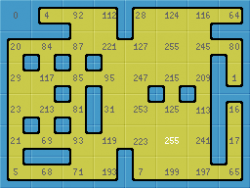
Basically, what you propose is to add variations of the 0 and the 255 tile. Because to the outside, the tile you add is identical to 0 and I assume its inverse would be identical to 255.
I dug up the old program and got it to compute an (optimally symmetric) 7x7 pattern which duplicates 0 and 255 instead of 255 twice. Attached (only the version without numbers because I am lazy).
Hi mawigator
OK ... neat idea, I like the way the 2 different styles of tile_0 can be shown.
btw, you might be better using the following template. It has all 16 Wang tiles, but opposite edges match too! So you can tile a plain which allows you to check all possible edge combinations. It is the only 4x4 layout which does this (besides rotations and reflections). It's called Brigid's Cross. See my site http://www.cr31.co.uk/stagecast/wang/pattern.html for more technical info on using Wang tiles.
Hi caeles
Very impressive. I love these computer 'brute force' solutions. Its amazing, I played around with a blob tileset for days but never found any of these neat layouts.
I drew out your 7x7 arrangement directly using the Stage tile explorer (on my cr31.co.uk website). The 2 blob brush tools need a bit of patience but do work. You can easily switch between different tilesets once drawn.
The tile index numbers are shown. Tile_0 does not have your central blob. I hope to design some more blob tilesets soon.
I'd be interested to know how many solutions there are. Is it hundreds or (as I suspect) just a few. Your new solution is composed of 2 islands. How many solutions retain a single land mass, or do any have more than 2 islands?
I appreciate such questions may not be easy to answer. But would be very interesting.
@ Guy:
Hundreds does not even start to describe the number of solutions. The solutions are sparse among the (mostly non-solution) configurations, that's why you couldn't find one manually. But they are numerous. So much, in fact, that I do not know the exact number. It would be infeasible to count them by brute force.
What I could do was to find solutions with one and three connected components (not counting the 0 tiles which, in my tileset, are connected components by themselves). Here they are in ASCII (use an even-width font like Courier to see them correctly):
o--o--o--o--o--o--o--o
|........|........|..|
|........|........|..|
o..o..o--o--o.....o--o
|....................|
|....................|
o..o........o.....o..o
|..|..............|..|
|..|..............|..|
o--o..............o..o
|..|.................|
|..|.................|
o..o..o........o.....o
|....................|
|....................|
o........o--o..o..o..o
|........|...........|
|........|...........|
o--o..o--o.....o..o..o
|..|.................|
|..|.................|
o--o--o--o--o--o--o--o
o--o--o--o--o--o--o--o
|..|.....|...........|
|..|.....|...........|
o..o--o--o........o..o
|..|..|..|...........|
|..|..|..|...........|
o--o--o--o--o.....o..o
|...........|........|
|...........|........|
o..o..o.....o........o
|....................|
|....................|
o.....o..o...........o
|....................|
|....................|
o..o..o..o........o..o
|.................|..|
|.................|..|
o..o........o..o--o..o
|....................|
|....................|
o--o--o--o--o--o--o--o
Thanks for the very quick solutions. They are quite neat. All connected I think is better. I just drew out your 'ASCII artwork' to help visualise them.
While you still have the old program out, I was wondering if there are any solutions which use every tile, except tile_0, just once? Because, if you create a set of puzzle tiles, you could produce just 46 tiles (not so prime and a bit cheaper than 47) which could be formed into a single island.
Or you could just have a seamless background of tile_0 and generate islands on top with just 46 tiles. I notice all solutions so far use duplicate tile_255's. Maybe this is necessary.
No, duplicating tile 255 is not essential. For certain template sizes duplication of something is necessary. I always chose 255 among the duplicates, because from the tileset design perspective it is a plausible candiate for need of variations. I expect duplicating any other tile instead works just as well for generating templates.
True, 46 is not a prime. Still, a 2 by 23 template does not appeal much to me. In any case one would have to sacrifice one property that all templates had so far: The border was always empty. With a height (or width) of only 2 the property could not be maintained, because otherwise there would be no place for tiles like 85.
Going for 45 tiles (no 0 and no 255) instead works better:
o--o--o--o--o--o--o--o--o--o
|...........|..|...........|
|...........|..|...........|
o.....o..o--o..o..o........o
|..........................|
|..........................|
o..o.....o--o...........o..o
|..|.....|.................|
|..|.....|.................|
o..o.....o--o..o..o.....o..o
|...........|..............|
|...........|..............|
o.....o..o..o..o..o........o
|...........|..|...........|
|...........|..|...........|
o--o--o--o--o--o--o--o--o--o
All cool stuff.
But, is there say a connected 7x7 island with 3 tile_0's. This is what I meant in my previous post. Sorry, I may not have explained it too clearly.
The island can be any shape and contain as many tile_0's as required to 'pack it out' into a neat square or rectangle. A bit like your first island solution but with 1 more tile_0 and 1 less tile_255.
Sorry for misreading you. Yes, that is possible:
o--o--o--o--o--o--o--o
|..|..|..............|
|..|..|..............|
o--o--o--o.....o--o--o
|..|.................|
|..|.................|
o--o...........o..o..o
|..|.................|
|..|.................|
o..o........o........o
|...........|........|
|...........|........|
o.....o..o--o--o.....o
|...........|........|
|...........|........|
o..o..o.....o..o..o..o
|..|.................|
|..|.................|
o..o..o........o..o..o
|..|.................|
|..|.................|
o--o--o--o--o--o--o--o
o--o--o--o--o--o--o--o
|..|..............|..|
|..|..............|..|
o--o--o--o.....o--o--o
|..|.................|
|..|.................|
o..o...........o..o..o
|..|.................|
|..|.................|
o..o........o........o
|...........|........|
|...........|........|
o.....o..o--o--o.....o
|...........|........|
|...........|........|
o..o..o.....o..o..o..o
|..|.................|
|..|.................|
o--o..o........o..o..o
|..|.................|
|..|.................|
o--o--o--o--o--o--o--o
o--o--o--o--o--o--o--o
|..|..............|..|
|..|..............|..|
o--o--o..o.....o--o--o
|..|.................|
|..|.................|
o..o...........o--o..o
|....................|
|....................|
o..o........o........o
|...........|........|
|...........|........|
o.....o..o--o--o.....o
|...........|........|
|...........|........|
o..o..o.....o..o..o..o
|..|..|..............|
|..|..|..............|
o--o..o........o..o..o
|..|.................|
|..|.................|
o--o--o--o--o--o--o--o
o--o--o--o--o--o--o--o
|..|..............|..|
|..|..............|..|
o--o--o........o..o--o
|..|...........|.....|
|..|...........|.....|
o..o..o..o.....o..o--o
|....................|
|....................|
o.....o..o--o........o
|........|...........|
|........|...........|
o........o........o..o
|....................|
|....................|
o..o--o..o........o..o
|.................|..|
|.................|..|
o--o..o.....o..o--o..o
|..|..|..............|
|..|..|..............|
o--o--o--o--o--o--o--o
Wow!! Yes - this is exactly what I hoped existed.
I've drawn them out to better appreciate their beauty and (almost) perfect symmetry. It's the 'almost' that drives you potty when trying to find such layouts by hand.
So, a puzzle of 46 shaped pieces could be formed into a single connected island. Maybe into the 7 by 7 lid of the box the puzzle came in. A perfect Blob island.
Many thanks Caeles for your exhaustive searches and no doubt some fine maths :-))
Does anyone have a 15 tile version of this layout for tiles without perspective that can get rotated?